5 Pewniaków na Egzamin Ósmoklasisty

Egzamin Ósmoklasisty z matematyki: 5 zadań, które pojawią się na 100%

Lista Pewniaków CKE:

✓
Działania na potęgach i pierwiastkach: Zadania zamknięte (zawsze 1-2 pkt).
✓
Twierdzenie Pitagorasa: Król geometrii. Bez niego ani rusz.
✓
Procenty w praktyce: Podwyżki, obniżki, cena brutto/netto.
✓
Równania z treścią: Zadanie otwarte za wysoką punktację.
✓
Rachunek Prawdopodobieństwa: Proste zadanie z losowaniem kul lub liczb.

1. Potęgi i Pierwiastki (Zadania Zamknięte)

Na samym początku arkusza zawsze trafisz na zadanie sprawdzające, czy znasz własności działań na potęgach. Nie musisz nic liczyć na kalkulatorze – musisz uprościć wyrażenie.

Działanie	Wzór uproszczony	Kiedy stosować?
Mnożenie	$a^x \cdot a^y = a^{x+y}$	Gdy na dole jest to samo (dodajemy góry)
Dzielenie	$a^x : a^y = a^{x-y}$	Gdy na dole jest to samo (odejmujemy góry)
Potęgowanie	$(a^x)^y = a^{x \cdot y}$	Gdy mamy nawias (mnożymy wykładniki)

Uwaga na pułapkę! Wzór

a^x \cdot b^x = (a \cdot b)^x

działa, gdy wykładniki są takie same.

Typowe zadanie egzaminacyjne:

Uprość wyrażenie:

\frac{(3^4)^3 \cdot 3^2}{3^5}

Rozwiązanie: 1. Najpierw nawias:

(3^4)^3 = 3^{12}

2. Góra ułamka (mnożenie):

3^{12} \cdot 3^2 = 3^{14}

3. Dzielenie przez dół:

3^{14} : 3^5 = 3^{14-5} = 3^9

Odpowiedź:

3^9

💡

Nigdy nie próbuj tego wyliczać (np. 3 razy 3 razy 3...). Operuj tylko na małych cyferkach u góry!

Pewniak z pierwiastkami (Wyłączanie czynnika):

Zadanie: Która liczba jest równa

\sqrt{72}

? A)

6\sqrt{2}

36\sqrt{2}

2\sqrt{6}

Rozwiązanie: Musisz rozbić liczbę 72 na mnożenie dwóch liczb, z których jedna ma pierwiastek.

\sqrt{72} = \sqrt{36 \cdot 2}

Wiemy, że

\sqrt{36} = 6

, więc wyrzucamy szóstkę przed nawias:

= 6\sqrt{2}

Odpowiedź A.

💡

Szukaj takich liczb jak: 4, 9, 16, 25, 36. To one pozwalają uprościć pierwiastek.

2. Twierdzenie Pitagorasa

W geometrii na egzaminie ósmoklasisty prawie zawsze pojawia się trójkąt prostokątny. Może być ukryty w trapezie, rombie albo w zadaniu praktycznym.

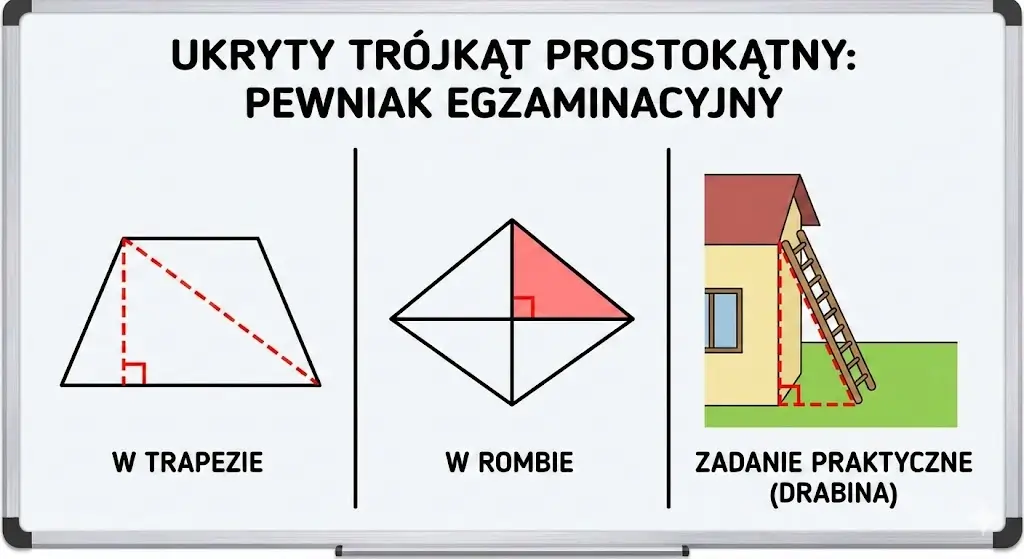
Pewniak geometryczny:

Wzór:

a^2 + b^2 = c^2

Zadanie: Przyprostokątne mają długość 3 i 4. Oblicz przeciwprostokątną.

3^2 + 4^2 = c^2

9 + 16 = c^2

25 = c^2

c = \sqrt{25} = 5

💡

Szukaj trójkątów pitagorejskich: (3, 4, 5), (6, 8, 10), (5, 12, 13). Często pojawiają się w zadaniach zamkniętych.

2.5. Procenty – Najszybsze punkty

Zadania z procentami są podchwytliwe, jeśli liczysz je na piechotę. Najważniejszy trik? Zamień procent na ułamek dziesiętny i Mnóż!

Treść zadania	Jak to zapisać?	Przykład
Oblicz 20% z liczby x	0,20 * x	20% z 50 to 10
Cena wzrosła o 20%	1,20 * x	Było 100, jest 120
Cena zmalała o 20%	0,80 * x	Odejmujemy od 100%. Zostaje 80%.

Zapamiętaj: Słowo z w matematyce prawie zawsze oznacza mnożenie.

Zadanie z podwyżką:

Smartfon kosztował 2000 zł. Jego cenę obniżono o 10%, a potem podwyższono o 10%. Ile kosztuje teraz?

Pułapka: To NIE jest znowu 2000 zł!

1. Cena po obniżce (zostało 90%):

2000 \cdot 0,9 = 1800 zł

2. Cena po podwyżce (mamy 110% nowej ceny):

1800 \cdot 1,1 = 1980 zł

**Odpowiedź:** 1980 zł.

💡

Zawsze licz krok po kroku. Procenty liczymy od AKTUALNEJ ceny, a nie od początkowej.

3. Równania z treścią (Zadanie Otwarte)

To zazwyczaj zadanie za 3-4 punkty. Najważniejszy jest pierwszy krok: oznaczenie niewiadomej x.

Schemat rozwiązywania:

📝 Schemat rozwiązywania

Przeczytaj zadanie uważnie 2 razy (zrozumienie to klucz!).

Oznacz niewiadomą (np. napisz: x – cena bułki).

Zapisz pozostałe dane z treści zadania za pomocą x.

Ułóż równanie, rozwiąż je i sprawdź wynik.

Przykład (Wiek):

Treść: Ala jest 3 razy starsza od Oli. Razem mają 40 lat. Rozwiązanie:

x

– wiek Oli

3x

– wiek Ali (bo 3 razy starsza) Równanie:

x + 3x = 40

4x = 40 \quad /:4

x = 10

Odpowiedź: Ola ma 10 lat, Ala ma 30 lat.

💡

Zawsze na końcu sprawdź wynik z treścią zadania. Czy 10 + 30 daje 40? Tak. Masz pewność, że jest dobrze.

4. Rachunek Prawdopodobieństwa

Brzmi strasznie, ale na poziomie ósmoklasisty to najprostsze zadanie w arkuszu. Wystarczy znać jeden główny wzór, który pozwoli Ci obliczyć szansę na dowolne zdarzenie.

Wzór na prawdopodobieństwo:

✓ $P(A) = \frac{\text{ILE PASUJE}}{\text{ILE JEST WSZYSTKICH}}$

Zadanie z kulami:

W pudełku są 3 kule białe i 7 czarnych. Jakie jest prawdopodobieństwo wylosowania kuli białej? Rozwiązanie krok po kroku: 1. Ile jest wszystkich kul w pudełku? (to będzie nasz mianownik)

3 + 7 = 10

2. Ile kul pasuje do treści pytania? (mamy 3 kule białe, więc to nasz licznik)

3

3. Podstawiamy do wzoru:

P(A) = \frac{3}{10} = 0,3

Odpowiedź: Prawdopodobieństwo wylosowania kuli białej wynosi 0,3 (lub 3/10).

💡

Pamiętaj, wynik prawdopodobieństwa musi być liczbą między 0 a 1. Jeśli wyjdzie Ci więcej niż 1, szukaj błędu w mianowniku!

5. Geometria Przestrzenna: Pudełka, Kostki i Akwaria

Zadania z bryłami (graniastosłupy) są pewne. Często dotyczą przelewania wody lub układania sześcianów. Musisz znać dwa wzory i jedną magiczną zależność.

[Image of volume of rectangular prism formula diagram]

Wielkość	Wzór ogólny	Uwagi
Objętość (V)	$V = Pp * H$	Pole podstawy razy wysokość.
Pole powierzchni (Pc)	$Pc = 2Pp + Pb$	Dwa razy podłoga plus ściany boczne.
Magiczna zamiana	$1 litr = 1 dm^3$	Zadania z wodą wymagają zamiany cm na dm!

Najczęstszy błąd? Liczenie objętości w centymetrach, gdy pytają o litry.

Pewniak z wodą:

Do akwarium o wymiarach podstawy

20 cm \times 30 cm

wlano 3 litry wody. O ile podniósł się poziom wody? 1. Zamieńmy jednostki na dm (bo

1 litr = 1 dm^3

20 cm = 2 dm

30 cm = 3 dm

. 2. Pole podstawy:

P_p = 2 \cdot 3 = 6 dm^2

3. Wzór na objętość (

V = P_p \cdot H

3 = 6 \cdot H

H = \frac{3}{6} = 0,5 dm = 5 cm

Odpowiedź: Poziom wody podniósł się o 5 cm.

💡

To zadanie pojawia się w różnych wariantach prawie co roku!

6. Prędkość, Droga, Czas (Fizyka w Matematyce)

Pociągi, rowery i żółwie. Kluczem jest trójkąt zależności: $s = v \cdot t$ (Droga = Prędkość razy Czas).

Pułapki czasowe (Uważaj!)

✓**Nigdy** nie zapisuj 15 minut jako 0,15h! To błąd.
✓15 minut to kwadrans, czyli $\frac{1}{4} h = 0,25 h$ .
✓Aby zamienić m/s na km/h, pomnóż przez 3,6.
✓Aby zamienić km/h na m/s, podziel przez 3,6.

Obliczanie średniej prędkości:

Adam przebiegł 600 metrów w 2 minuty. Jaka była jego średnia prędkość w km/h? 1. Zamieńmy na podstawowe jednostki (

km

h

): Droga

s = 0,6 km

. Czas

t = 2 min = \frac{2}{60} h = \frac{1}{30} h

. 2. Wzór (

v = \frac{s}{t}

v = \frac{0,6}{\frac{1}{30}} = 0,6 \cdot 30 = 18

Odpowiedź:

18 km/h

💡

Dzielenie przez ułamek to mnożenie przez odwrotność. To kluczowa umiejętność!

7. Geometria Płaska: Kąty i Wielokąty

Geometria to nie tylko Pitagoras. Musisz znać własności kątów. Zadania często polegają na „gonieniu kątów” po rysunku.

Pamiętaj:

Suma kątów w trójkącie: Zawsze $180^\circ$
Suma kątów w czworokącie: Zawsze $360^\circ$
Kąty przyległe: Leżą na jednej prostej, ich suma to $180^\circ$
Kąty wierzchołkowe: Leżą naprzeciwko siebie, są równe.

Zadanie z trójkątem równoramiennym:

Trójkąt jest równoramienny. Kąt przy podstawie ma

70^circ

. Oblicz kąt między ramionami. 1. W trójkącie równoramiennym kąty przy podstawie są takie same. Więc drugi też ma

70^\circ

. 2. Suma to

180^circ

180^\circ - (70^\circ + 70^\circ) = 180^\circ - 140^\circ = 40^\circ

Odpowiedź:

40^\circ

💡

Słowo 'równoramienny' to ukryta dana liczbowa. Nie przegap jej w treści zadania!

🛡️ Strategia: Jak nie stracić punktów?

Kilka „hacków”, które uratują Twój wynik, gdy stres weźmie górę.

⚠️

Pułapka w Jednostkach

Zawsze sprawdzaj, czy nie ma haczyka (np. jeden bok w cm, drugi w dm). Musisz je ujednolicić przed liczeniem!

💎

Darmowe punkty w otwartych

Nawet jeśli nie umiesz rozwiązać zadania do końca, napisz dane i założenia oraz zrób rysunek. Często za samo wypisanie danych dostajesz +1 pkt (nawet przy złym wyniku!).

➗

Zwykłe czy Dziesiętne?

🛒 Sklep (pieniądze): Używaj dziesiętnych (np. $12{,}50$ ).

🍰 Algebra (wzory): Używaj zwykłych (np. $\frac{1}{3}$ ). Łatwiej się skracają!

🔓

Złam szyfr egzaminu

Pamiętaj: Egzamin ósmoklasisty to nie matura – zadania są tutaj bardzo schematyczne i powtarzalne. Nie musisz być geniuszem, wystarczy, że będziesz sprytny.

Przerób po 5 zadań z każdego wymienionego działu, a gwarantuję, że Twój wynik wzrośnie o 20-30%.

📚 Rozpocznij trening w Bazie Wiedzy →

W Bazie Wiedzy znajdziesz darmowe pewniaki i rozwiązania krok po kroku.

Masz problem z tym tematem? 🤯

Samodzielna nauka bywa trudna. Zapisz się na darmową próbkę, a opiszemy Ci plan działania w 15 minut – prosto, konkretnie i bez stresu.

🚀 Umów darmową konsultację

Autor: Alan Ostrowski Julian Lewicki

Ostatnia aktualizacja: 2026-02-01